L
LabZero
Thread author
Hello
Introduction
Write the introduction is always the hardest part, because it always ends up that the reader becomes bored with things that already expects.
In this tutorial we will discuss assembly language. Have a great familiarity with this language is essential because, not having available sources of malware files that you want to analyze, the disassembler listing (or debugger) is the only thing you have.
For those who want to learn to program in assembly language, here you will find enough information to get an idea of how things work, but not so many that you can start writing code.
The tutorial is divided into two parts: in the first we will see the synthesis processor architecture; in the second, more substantial and can be used as a simple reference manual, we will analyze all statements.
Prerequisites
It would be nice if anyone could understand this tutorial, but you can't help but consider some prerequisite.
You need a good familiarity with the binary and hexadecimal numbering and changes from a base to the other; to those who had not familiar with these concepts suggest you return here after reading some tutorials about it.
Well, let's start now to analyze the AMD64 architecture (henceforth simply x 64). Let's start with the first part a bit more where we see no theoretical even a line of code; I promise that I will try to be brief. In the second part we will see all the basic instructions and ... the code will arrive.
Essay
x 86 and x 64
The x 64 architecture is essentially an extension of the previous Intel IA32 architecture, which is present in all PCs from the 80386. In the standard size IA32 operand was 32 bits (as in the past had been to 16 bit); x 64 architecture general purpose registers (and memory addresses) are 64 bits long.
The introduction of 64-bit processors, the AMD64 wasn't the only competitor in the game, since the Intel IA64 his proposed a completely different, but renounced the backward compatibility (i.e., compatibility with previous processors). As is known, in computer science, the sacredness of this principle cannot be put into question; the AMD64 has caught on and, now, even the Intel has made substantially its compatible processors (Intel and AMD's implementation has many names: EM64T, Intel 64, Intel IA32e).
From now on I'll use x 64 and x 86 names indicate, respectively, the AMD64, IA32. The term x 86-16 will be used for the 16-bit architecture of the intel processors prior to the IA32 (i.e. from Intel 8086 Intel 80286).
The bit and its multiples
Know all the equivalence 1 byte = 8 bits. Byte multiples more commonly used are as follows:
Word = 2 bytes = 16 bits
DWORD search (dword) = 2 word = 4 bytes = 32 bit
quadword (qdord) = 2 = 4 word dword = 8 bytes = 64 bits
More rarely you hear of oword (octaword), i.e. 2, also called double quadword quadword; sometimes fword (6 bytes) or even terabytes (ten bytes, 10 bytes).
Unsigned integers and sign
Integers can be of two types: unsigned (unsigned integers) or signed (signed integers). The size of integers can be 8, 16, 32, 64 bits; more rarely, 128 bit (in multiplication and Division in x 64).
An unsigned integer to n bits can represent all numbers between 0 and 2n-1. So an 8-bit unsigned integer that is at most 255, 16 bit is worth a maximum of 65535, to 32 bits over 4 billion, 64 bit more than 18 billion billion. The binary representation is usual, for which the largest number that can represent is that consisting of all bits 1.
A signed integer with n bits, instead, can represent all numbers between 2n and 2n-1-1-1. 8 bit so you go from -128 to +127, 16 bits from -32768 to +32767, to 32 bits from a smaller number of -2 billion to more than 2 billion, to 64 bits by a number less than -9 billion billion to more than 9 billion billion.
Signed integers using a representation known as 2 's complement. The representation of positive numbers (and zero) remains the same; However, since positive numbers are limited to half of the possible n bit values, all (and only) non-negative numbers have the most significant bit ("leftmost") equal to 0; the numbers with the most significant bit is 1, the negative numbers. The most significant bit is called, for this reason, sign bit. In whole to 8, 16, 32, 64 bit, the sign bit has 7 index, respectively, 15, 31, 63.
The binary representation of a negative number by 2 's complement is very easy to get: represent in binary the number negative-x, just write x, reverse all his bits, then add 1. For example, working with 8 bit, suppose we want to write -6. The binary representation of is 00000110 6 (write the initial zero bits to emphasise that we are using 8 bit). Inverting all the bits you get 11111001; adding 1 you get 11111010. This is the 8-bit binary representation of -6. We note an important property: adding 6 representations and -6 you get 100000000, which in decimal is equivalent to 256; This number has 9 bits, if we cut to 8 bits we get 0 (because the size of the processor's operations always has a fixed number of bits, the truncation is implied). The fact that the sum of two opposite numbers 0 face is crucial, and in this consists the usefulness of 2 's complement.
It is better to acquire a good familiarity with these concepts.
Zero-extension and sign-extension
Arithmetic operations between numbers represented by the same number of bits are usual manner; It happens, however, often having to perform between operands of different size. In this case, the smallest size operand must be converted (implicitly or explicitly) to the right size.
In the case of transactions between unsigned integers, this is trivial: simply prefix the number of smaller size a 0 bit as many need to get the right size: the representation of 6 to 8 bit is 00000110, 16 bits is 0000000000000110. This process is called zero-extension.
In the case of signed integers, however, this does not work. More precisely, it only works for positive numbers. But the -6 representation is 11111010, with zero-extension 0000000011111010 is obtained, i.e. 250 decimal: not exactly the same thing. The reason lies in the special meaning of the sign bit and operation of 2 's complement. The representation of a 16 bit -6 is 1111111111111010, i.e. the extending 8 bits with 1 instead of 0. In General, the extension of signed integers is done filling all the bits with values equal to the sign bit. This mechanism is called sign-extension.
The registers
Inside the CPU there are a large number of registers for different functions. A log is only a memory cell, the fastest in the processor. They are used to store the State of the processor, continually modified as a result of execution of instructions.
Let's see first how is composed the register set of the x 86 architecture, and then see how it was extended in x 64.
X 86 registers
A first group of records consists of General Purpose Registers (GPRs), i.e. the General purpose registers, called so because, ideally, can be used for any purpose.
The General format of a general purpose register (let's take as example EAX) is as follows:

The lines should imagine how overlapping: the entire register is EAX, 16 bits ("right" in the numeric representation) form AX, the 8 bits forming AL (the letter L stands for Low). The 8 most significant bits of AX form the AH register (where H stands for High).
There are 8 32 bit registers for general use: EAX, EBX, ECX, EDX, ESI, EDI, EBP, ESP. The namespace and was added with the introduction of the IA32 architecture as an extension of earlier than 16 bits.
Often it is used to indicate all logs in uppercase or all lowercase, while eAX notation with the first letter indicates either AX or EAX. Similarly, using the notations eBX, eCX, and so on.
EBX, ECX and EDX have the same format as seen above, little EAX so subregister of EBX are BX, BH, BL, ECX are CX, CH, CL, EDX, finally, DX, DH, DL.
Normally each of these logs can be used for any purpose, although there are a number of exceptions: we will analyse later. The register EAX is also called accumulator, more for historical reasons which, although there are a number of situations where its use is necessary and others where it is preferable to other registers. To a lesser extent, this is also true for EBX, ECX, EDX.
For other General Purpose registers in 32 bit (ESI, EDI, EBP, ESP) you cannot access subregister of 8 bits, while the subregister of 16 bits are, in order, Yes,, BP, SP.
ESI and EDI (whose acronyms are for Source and Destination Index Index) can be used for any purpose as the previous ones, but have a special support for use as indexes for operations on strings (scanning, copying, comparison). The respective subregister to 16 bits are THERE and, while there are subregister in 8 bits (as already pointed out).
EBP and ESP (Base Pointer and Stack Pointer) are used in the management of the stack (we'll delve into later). ESP indicates the current location onto the stack, while the base usually tip EBP stack, i.e., for instance, the area of memory where the local data of a function (normal procedure variables, not visible outside). Actually nothing prohibits using EBP for other purposes, but this is not very common. The counterpart to 16 bits are BP and SP.
Ultimately, the set of General Purpose Registers x 86 architecture provides:
8-byte registers (AH, AL, BH, BL, CH, CL, DH, DL);
8 a word records (AX, BX, CX, DX, IT, BP, SP);
8 1 dword registers (EAX, EBX, ECX, EDX, ESI, EDI, EBP, ESP).
A part is register EIP (with the IP subregister), the Instruction Pointer: it always points to the next instruction to be executed. EIP you can't read or write as other registries, but can be changed indirectly or with flow control statements that we will see below.
A very important log is the EFLAGS register. This log is a bit field, consisting of a large number of flags, values binary (0 or 1) with disparate purposes. Here's a diagram:
| | | 29 30 31 | 28 | | | 25 26 27 | | | 22 23 24 | 21 | | | 18 19 20 | 17 | | 16 15 14 13 12 | | | | 10 | 11 09 | | | 07 08 06 | 04 03 05 | | | | | 00 01 02 |

Apart from a number of flags, in fact, useful only for system programming, there are 6 (the status flags) that are set to 1 or 0 depending on the outcome of many instructions. It is essential to know.
Carry Flag (CF, bit 0)-carry Flag. Is put to 1 when there is a carry (in the case of a sum) or a loan (for subtraction) from the most significant bit of an operation. For example, EAX contains the hexadecimal value 0x9000000 and execute the instruction ADD EAX, EAX, the result (0x120000000) is truncated to 32 bits (0x20000000), and the presence of carryover is signalled by setting the Carry Flag to 1. Shift operations or, instead, the meaning is different, but we will see later.
Parity Flag (PF, bit 2)-parity Flag. Is set when the least significant byte of the result of many operations contains an even number of 1 bits. Is commonly used in data transmission systems such as control system; for anyone who is a novice may be sufficient to know existed. Actual use is quite rare.
Auxiliary Carry Flag (AF, bit 4)-is set to 1 when there is a carry or borrow a bit from the third operation of type BCD (Binary Coded Decimal), zero otherwise.
Zero Flag (ZF, 6 bits)-is set to 1 if the result of an operation is zero, otherwise it is cleared.
Sign Flag (SF, bit 7)-sign Flag. Is put to 1 if, after an arithmetic operation, the most significant bit (the sign bit) is 1. Otherwise it is cleared.
Overflow Flag (OF, bit 11)-is put to 1 when the result of an operation is too large (overflow) or too small (underflow) to be contained in the register of destination; is set to zero otherwise. More specifically, it is set to 1 if the sign bit (most significant) of the result is different from that of both operands. In the case of sums or subtractions is easy to be convinced that this condition is equivalent to an overflow/underflow.
The importance of status flags will be clear when we will analyze the flow control statements (but are useful for other instructions).
Another noteworthy flag (classified as control flag, since it alters the behavior of the processor) is the Direction Flag (DF, 10 bits). It allows you to decide the direction in which they are carried out on string operations, i.e. If the eSI and eDI registers are incremented or decremented at each repetition. Operations on strings will not be treated.
Special registers for memory management are the Segment Registers, 16-bit registers containing a segment selector. The segments allow you to manage segmented memory models (...), which were typically used multiprocessing systems to isolate each from other process transparently. They are CS (Code Segment), DS (Data Segment), ES (Extra Segment), FS, GS, SS (Stack Segment). The Code Segment is the segment containing the code, while others are for data segments; DS is the default for most (others to be used, must usually be indicated explicitly in assembler, which will encode them properly in the machine code). SS is the segment that contains the stack. FS and GS segments are more data whose names have no special meaning and should only continue the alphabetic sequence; were introduced in Intel 80386 processors.
Other registers used for advanced uses are the Debug Registers (DR0, DR1, DR2, DR3, DR6 and DR7), mainly used by debugger, and the Control Registers (CR0 at CR4), used only at the level of the operating system and by normal application ever.
X 64 registers
The AMD64 architecture is an extension of the IA32 designed to maintain backwards compatibility. X 64 processors can run in 32 bit applications in 64-bit operating systems, but may even act like 32-bit processors (and then run a 32-bit operating system). However, to really leverage the power of x 64 architecture is necessary to compile programs specifically for this architecture and own a 64-bit operating system, so that the processor can run at 64 bits.
In 64-bit mode, the x 64 processors provide a series of extensions.
All General Purpose Registers, the Instruction Pointer, the flags are large 64 bit instead of 32.
8 GPRs are added, for a total of 16. The lack of registers was one of the main reasons to rethink the architecture from x 86 to x 64.
The registers RAX, RBX become, RCX, RDX, RSI, RDI, RBP, RSP. The extended registers 8 are simply numbered from R8 to R15. For each register can also be accessed at sottoregistri by 32-, 16-, 8-bit content in the less significant. From RAX to RSP names are those already seen (e.g. EAX, AX, AL), but they become even addressable 8 bits of RSI, RDI, RBP, RSP, with SIL, DIL, BPL, SPL respectively. The subregister to 32, 16, 8-bit registers R8 to R15 themselves by adding the suffixes D, W, B respectively, which are of course for Dword, Word, and Byte. For example the subregister to 16 bits of R8 is called R8W.
You can still access the register AH, BH, CH and DH, but you cannot mix in a single statement these logs with extended ones (i.e. those that do not exist in the x 86 architecture).
Schematically, the GPRs becomes:
16 64-bit registers: RAX, RBX, RCX, RDX, RBP, RSI, RDI, RSP, R8, R9, R10, R11, R12, R13, R14, R15;
16 32-bit registers: EAX, EBX, ECX, EDX, EBP, ESI, EDI, ESP, R9D, R10D, R8D, R11D,, R13D, R12D, R14D R15D;
16 16-bit registers: AX, BX, CX, DX, BP, SI, to, R8W, R9W, SP, R10W, R11W, R12W, R13W, R14W, R15W;
formed from 8 registers 16 bits: logs, BL, CL, DL, BPL, DIL, SIL, R8B, R9B, SPL, R10B, R11B, R12B, R13B, R14B, R15B;
4 8-bit registers in the most significant bits of AX, BX, CX, and DX, namely: AH, BH, CH, DH.
The EIP register was extended in RIP, the EFLAGS register and extended in RFLAGS.
Unlike the x 86, x 64 architecture provides the ability to use RIP for addressing, i.e. to read or write to memory locations that are RIP up to 2 GB. We will see later on the details of addressing related to RIP.
RAX notation is often used to denote indifferently, EAX or RAX AX; similar notations exist for all other registers.
Segment registers are hardly used anymore in 64-bit mode, since the memory management using segmentation becomes superfluous if the pointer size is 64 bits (which means one address space of 264 bytes, i.e. really many). Are considered only the registers CS, FS and GS, but much less essential than in x 86. The other Segment Registers are simply ignored.
32-bit operations on x 64
In x 64, the default size of the operands is, for the most part, 32-bit instructions. Machine language encodings of the 64-bit versions of the instructions require the addition of a special prefix instruction encoding; This prefix enables access to the extended set of registers.
Unlike the subregister operations to 8 and 16 bit, acting only on the subregister leaving unchanged the other 56 48 bit, or changes to the 32-bit registers reset the 32 most significant bits of the register (in technical jargon, are zero-extended). For example, assuming that the initial state is the following:
Assuming the variants to 64, 32, 16 and 8 bit (the statement that adds the second operand to the first, saving the result in the first), you have the following options:
The second line is highlighted to emphasize the different behaviour of the 32-bit version than the other.
Memory
From the application viewpoint, the memory can be viewed as simply a set of contiguous bytes, each with its own address, which you can read or write. In fact, an address contained in a pointer is a virtual address (virtual address) that must go through phases of translation to get the physical address (physical address), i.e. the real address in memory. The translation takes place transparently to applications.
Segmentation
In models that use memory segmentation, each memory access (explicitly or implicitly) also a segment selector (contained in a Segment Register), used by the hardware to know where in memory segment (basis), how big is (limit) and the type of access allowed. Where access is outside the segment size or be of a type that is not allowed (e.g. writing a read-only segment), the hardware raises an exception to signal the abnormality (that, if not handled properly, causing the crash, i.e. the closure enforced by the operating system).
The segmentation was very common in older systems, but is almost out of use in modern x 86 systems, which use a flat memory model, with having segments 0 and base limit 4 GB, which is essentially disabling the segmentation; for this reason has been almost completely removed from the x 64 architecture.
Paging
Paging, instead, provides a protection system more homogenous, allowing you to specify the permissions for each page, i.e. a large block of memory, usually 4 kb (4096 bytes). It also allows you to remap any way physical memory that the application addresses consecutive believes (in the only place that knows, that virtual) can be in any position in RAM or, indeed, can be removed and stored in the hard drive to make room for something else, and will be in RAM when the application wants to access it again (thanks to modern operating systems paging can "emulate" more RAM than is actually there , albeit with a performance degradation). Everything happens transparently to the application.
Order of bytes
In the case of dimension data a byte (or composite data as ASCII strings, which are simply arrays of bytes) there is only one possible order in memory: each byte has its unique position.
However, in the case of dimension data word (2 bytes), dword (4 bytes) or qword (8 bytes) there are two main conventions: big-endian and little-endian.
In big-endian Convention, are written by more bytes significant to least significant, so that their simple concatenation form as complete. For example, if memory address 0x402000 is the dword, 0x11223344 memory were, in order, the bytes 0x11 (at 0x402000), 0x22 (at 0x402001), 0x33 (at 0x402002), 0x44 (at 0x402003). Big-endian notation is the standard for communication over the network, but is also used in some processors.
In little-endian Convention, instead of multiple bytes of the byte are written from most significant to least significant, i.e. in reverse order in memory. The 0x11223344 dword at 0x402000 would be stored as follows: 0x44 (at 0x402000), 0x33 (at 0x402001), 0x22 (at 0x402002), 0x11 (at 0x402003).
All x 86 and x 64 processors use little-endian Convention, so you have to get used to the bytes reversed.
An undoubted advantage of little-endian notation is this: the same data is represented and simultaneously correctly under different sizes. For example, the 0x00000055 dword at 0x402000 becomes: 00 00 00 55. Reading the word at the same address reads: 00 55, i.e. 0x0055 on little-endian; reading a byte 0x55 reads. This can be very convenient for those who program in assembly.
Some processor has also adopted more complicated notations (mixed-endian).
Stack
The stack is a region of memory available for each process to save temporary information.
A stack is a LIFO data structure (Last-In first-out), i.e. a structure in which information is removed in reverse order compared to that. The pointer to the last item pushed onto the stack is contained in the rSP register (i.e. in RSP if we x 64, x 86, ESP in SP in the old x 86-16). Segmented memory models in x 86, it is useful to know that the stack is contained in SS and that all references that contain rBP or rSP are made by default through the SS.
The stack can be used to store data in a register to be used later, in order to free the log for other purposes. The LIFO structure, the data is restored in the reverse order than how they were entered. If I saved, in order, RAX, RSI and R14, then restore first R14, CSR and then finally RAX. We will see later PUSH and POP instructions that are used to manipulate the stack.
Another stack function is to manage the flow control in procedure calls. When a procedure is called, in fact, you must save the address of the instruction from which to restart execution at the end of the procedure. This return address (return address) is implicitly saved on the stack from the CALL statement to call a procedure, and is removed from the RET statement that is always the last of a procedure.
The parameters passed to a procedure are sometimes placed on the stack by the caller (sometimes are, instead, passed through the logs ... just agree!). Finally, is that stack is reserved space for the local variables in a procedure (those that exist only during the execution of the procedure itself and cease to exist upon its completion).
We will return later to talk more in detail of stack, PUSH and POP instructions, flow-control statements and calling conventions.
The assembly language
Let's finally talk of assembly language.
The syntax that is used in this tutorial is the MASM assembler; However, it is not difficult to adapt the syntax to other assemblers, in which case please refer to the respective manuals to know the differences.
Basic syntax
The syntax of assembly instructions is in general very simple. Each statement has a name that is mnemonic because basically said just need to remember not the binary encoding in machine language. The numeric code that represents the statement has said opcode (operation code contraction).
Each statement can have 0, 1 or 2 operands; in rare cases 3. The complete statement, in a separate line in the source file, is formed by the mnemonic and the list of its operands. Between the mnemonic and the operand list, of course, it takes at least one space; operands are separated by commas. For example the ADD statement has two parameters, which (among other things) can be two registers. A statement is valid:
This sum statement register rbx, rax register saving the result in rax. We can already highlight a constant of all statements with two operands: if it makes sense to talk about source and destination (i.e. the operand in which the processor saves the result), the MASM syntax requires that the destination is always the first operand (assemblers exist that use the AT&T syntax with the operands reversed; they are more used in Linux environment). So many instructions will be of the type:
mnemonic dst, src
The number and type of its operands are specified in detail in the manuals (see bibliography), but for all the basic instructions we will see them later.
Types of operands and synopsis
The instructions may require different types of operands. The main ones are the following: a register, a value in memory, an immediate (i.e. a numeric constant) or relative (i.e. going in all the Instruction Pointer).
The operands may be of different sizes, so afterwards, when we describe the synopsis of the instructions always specify what are those allowed.
Let's start with some general remarks on the assembly and on the format of the instructions; This section continues with a long introduction to assembly instructions: we will analyse, with a certain degree of detail, some forty assembly instructions: a relatively small subset compared to the hundreds of existing instructions, but that covers almost all the instructions that you will encounter in practice.
Don't worry about memorizing everything immediately, is not required; This is possible (and actually quite easy) only with practice. But don't be in a hurry to go to the next section.
Size of operands in memory
Operands in memory, are indicated in MASM, but also in the many listing disassembler, enclosed in square brackets. For example, the instruction MOV RAX, [RBX] copy in RAX the qword contained the memory address pointed to by RBX. We observe that the second operand contains no information about size; However, in the MOV the two operands have the same size, and the size must be the same, i.e. 64-bit RAX. In other cases, however, there would be ambiguity; for example education INC. [RBX], which increases the value pointed to by EBX, exist in 8, 16, 32, 64 bits. In this case, both x 86 x 64 that the default size is 32 bits. To indicate a size other than the default, it prepends an associative expression as "byte", "word ptr ptr, dword ptr" "" or "qword ptr". For example INC. bytes ptr [ebx] increments the byte pointed to by qword ptr INC ebx, [ebx] increments a qword, and so on.
The General addressing format an operand in memory (i.e. What can be contained in square brackets) on x 86 is as follows:
base + index * scale + displacement
Where base and index are two 32-bit registers (but cannot be ESP index), the scale factor may be 1, 2, 4 or 8 (if 1 is obviously not shown), the displacement is an integer with the score at 8, 16 or 32 bits. For example,:
mov rdx, qword ptr [ebx + ecx * 8 + 24]
In x 64 you can use the same type of addressing, index-based, stairs and displacement; base and index are usually general purpose registers any to 64 bits, but you can also use 32-bit registers (but not one to 64 and 32 bit, of course), in which case you can address only part of the address space (4 GB). The displacement is a signed integer of 32 bits, so it is no longer possible to type a mov eax, [address] where address is an absolute address in memory.
x 64 introduces a form of addressing not present on x 86: addressing related to RIP (in Italian is not that great, English speakers say RIP relative addressing). In this case, you have only a displacement of 32 bits the processor adds to RIP the next statement. In this way you can address data which are up to 2 GB RIP, which is usually enough for normal applications (an executable image fails virtually never this size!). An advantage of this form of addressing is to make the code independent of its actual location in memory, while with absolute addresses a possible relocation (i.e. uploading to an address other than the one provided) requires the correct loader absolute addresses (although, in reality, this operation has never been particularly expensive).
Data alignment
In-memory data should always be aligned. A data is properly aligned when its in-memory address is a multiple of its size (I refer here solely to data whose size is a power of 2). So for a b there are never problems, but a word should be in an address divisible by 2 (i.e. the last bit 0), a dword in an address divisible by 4 (the last two bits are 0), a qword an address divisible by 8 (last three 0 bits), and so on.
Why is convenient to align the data is the gain in efficiency: so the processor accesses them more quickly. Access to a dword is not aligned, for example, requires the processor to make two requests to memory instead of one.
In 64-bit Windows, however, the alignment is required stack API calls, so it becomes more than a mere performance issue.
The MOV instruction
The MOV instruction is one of the main and most common assembly instructions. The General format is:
and what education does is copy in dst data that are contained in the src. The two operands are not necessarily the same size.
In its simplest form, dst and src are registers or records and an operand in memory (but not two operands in memory):
If dst is a register to 8, 16, 32 or 64 bit, src may also be an immediate of the same size. If dst is an operand in memory of 8, 16, 32 bit, src can be an instant of the same size, while if dst is an operand in memory to 64 bit, src may still be an immediate 32-bit signed that is extended with the sign (sign-extended) to 64 bit and copied to dst.
If dst is AL, AX, EAX or RAX, you can also read a memory value at a given address to 64 bits (of course, you can do only x 86 with a 32-bit address). Mov is the only statement that can have a value as an operand in memory with an address to 64 bits.
Of course, in practice it happens very rarely write the address in this way, since you can use the RIP-relative addressing. In x 86, however, this is quite common for accessing global data.
Conversely, if src is AL, AX, EAX or RAX, dst can be a value in memory that is given the address (example: mov byte ptr [1122334455667788h], al).
There are also variants of the MOV instruction to read or write the Segment Registers, Debug Registers or Control Registers.
The MOV instruction does not change the RFLAGS log.
PUSH and POP instructions
Push and POP are the two main instructions to manipulate the stack. Both take a parameter; PUSH to insert something in the stack, POP to pop it.
The PUSH decrements rSP register to a value of 8 in x 64, 4 in x 86; then save the value of the operand to the address pointed to by rSP. The operand can be either a PUSH registry, a value in memory or immediate. In x 64, the immediate cannot be 64 bit, but may be a signed integer to 32 bit which is sign-extended and put onto the stack as 64-bit value.
The PUSH with 32 bit working is the rule on x 86, but does not exist in x 64. Exists in both PUSH education architectures with working at 16 bit, but usually has little sense because it leaves the stack unaligned (but, for example, nothing prevents to use 16-bit 4 to PUSH and withdraw later one qword).
The POP instruction operand is a register or a location in memory of 16, 32 or 64-bit (32-bit version does not exist in x 64 x 86; instead, there is obviously the 64-bit version).
POP copies the value onto the stack in the destination operand, and then increments the rSP (8, 4 or 2 for POP to 64, 32, 16 bit).
The beginners are often confused by the fact that PUSH (= put something stack) decrements rSP, while POP (= take away something from the stack) the increments. The stack grows backwards, so it's good to get used to.
Push and POP are often used, to save one or more values on the stack and restore them later:
Note that the order of POP is back than PUSH.
The PUSH is also used to pass parameters to a function call, when they are not passed through the logs (we will see later calling conventions).
To delete one or more elements from the stack without reading them, you can simply use the ADD instruction (add 8 * n bytes for RSP in x 64 is equivalent to removing n elements).
LEA
The LEA instruction (Load Effective Address) is connected, in a way, to the MOV. LEA takes two parameters, the first is a record to 16, 32 or 64 bits. The second is a value in memory.
In fact, the operand is in memory only, since, in fact, there is no access to the RAM of the processor. LEA in the copy destination only operand address in memory. (example)
The last example shows the use of LEA to make simple calculations that, Alternatively, would require more than one statement. LEA also has the desirable properties, sometimes, do not change any of the flags.
In fact, the first operand and size the size of the registers used in addressing the second operand may be different. If the first operand is smaller, the result is truncated; If it is larger, is zero-extended:
XCHG
The XCHG instruction (eXCHanGe) requires two operands, which can either be two registers, or a register and an operand in memory. The two operands can be great 8, 16, 32 or 64 bit, but must have the same size. The XCHG instruction swaps the values of the two operands.
NOP
The instruction NOP (No OPeration) is the simplest that there is ... In fact, his job is to do absolutely nothing (apart, obviously, increase rIP to pass to the next statement!). The opcode 0x90 the NOP instruction is one byte; This makes it particularly useful for reverse engineering purposes . To counteract a statement (such as a conditional jump statement) you can replace it with a series of longtime NOP exactly how the statement (delete the instruction, in fact, would compromise the file alignment).
Mathematical statements
ADD and SUB
ADD and SUB instructions allow you to perform addition and sums. The General format is:
where dst can be a log or a value in memory, src records, a value in memory or an immediate large signed up to 32 bits (the limit also applies if dst is great 64 bit). src and dst, however, cannot be both operands in memory, and must be the same size (except the case where src is an immediate, in which case, if it is smaller, it simply extended with the sign to be added/subtracted to dst). Examples:
If the second operand is immediate, both statements have shorter encodings if the target is AL, AX, EAX or RAX.
Both the ADD statement that the SUB statement change all the status flags 6 in a concorde to the result of the operation.
Sometimes the SUB statement is used to clear a log by removing himself, but for this purpose it is recommended (and more common) the logical XOR instruction.
NEG
The NEG instruction (Denied) has only one operand, a register or memory value to 8, 16, 32 or 64 bits; NEG make the 2 's complement of its operand, i.e. calculates the opposite. Of course it only makes sense for signed integers.
NEG sets the Carry Flag to 0 if the value of the operand is 0, otherwise sets it to 1. Other status flags (OF, SF, ZF, AF and PF) are set according to the result.
ADC and SBB
The instructions and SBB ADC (ADd with Carry respectively and SuBtract with Borrow) have the same syntax to ADD and SUB, but also the same function. The only difference is that ADC adds 1 to the result further if the Carry Flag is 1; Similarly, SBB subtracts 1 if the CF is 1. Instead behave exactly like ADD and SUB If CF is 0.
Instructions ADC and SBB serve to take account of the carry (carry) or loan (borrow) in the case of additions or subtractions in several parts. For example, if you want to add RAX: RBX (i.e. the concatenation of RAX, RBX and a 128-bit number) with RCX: RDX, you can use the following code:
For subtraction, instead:
Inc and DEC
Inc and DEC (INCrement and DECrement) have only one operand, which can be either a register or a memory operand. The effect of these instructions is to add (INC) or subtract (DEC) 1 to the operand, such as ADD and SUB instructions where the second operand is 1. Have a shorter encoding.
The only difference is that ADD and SUB keys INC and DEC preserve the Carry Flag; all other flags are changed in the same way.
MUL and IMUL
The MUL and IMUL instruction (MULtiply) are used to perform the multiplications, or unsigned integers.
The MUL instruction has only one operand, a register or memory value to 8, 16, 32 or 64 bits. Depending on the size of the operand, MUL performs the product between its operand, and a value of AL, AX, EAX or RAX, respectively; the result is saved in AX, DX: AX, EDX: EAX, RDX: RAX, where the notation with colons indicates concatenation. Target logs have a double size because, in General, the product of two n-bit numbers need 2n bits to be entirely content. Examples:
The IMUL instruction is more flexible, and can occur with one, two or three operands.
In form to an operand (register or memory value to 8, 16, 32 or 64 bit), multiplies the loperando IMUL value of AL, AX, EAX or RAX (depending on the size of the operand) and save the result in AX, DX: AX, EDX: EAX or RAX RDX:; in other words, it works as MUL, except that multiplication is done considering the operands as signed integers. Example:
In form to two operands, the first is the destination, a register to 16, 32 or 64 bits, and the second a register or memory value of equal size, or an immediate value (if the smaller immediate operands, is sign-extended; if the operands are of 64 bit, the immediate is at most 32-bit anyway). In this case the target is multiplied by the second operand and the result is saved in the destination.
In form three operands, the first is the destination, a register to 16, 32 or 64 bits; the second is a register or memory value of equal size; the third is an immediate (again, if the 8-bit immediate operands are larger, the immediate is sign-extended; are not allowed immediate 64 bit). The statement then multiplies second and third operand, and stores the result in the first.
We observe that in two and three operands, the destination is not bigger, so if the result is too large to fit in the destination, you would get only half less significant.
In the case of MUL or IMUL with an operand, the Carry Flag, Overflow Flag and are put to 1 if half of the result is different from 0, and are set to zero otherwise. For shapes in two and three operands of IMUL, CF and OF are 1 in case of overflow, i.e. If the result is larger than the destination register (in fact not much different from the case at 1 operand).
Other flags status (SF, ZF, AF and PF) are undefined after MUL, IMUL or so you should not rely on their value.
Div and IDIV; CBW, CWD, CDQ, CQO
DIV and IDIV instructions perform the divisions, respectively without and with mark. Both statements take a single operand, a register or memory value to 8, 16, 32 or 64 bits that represents the divisor. The dividend is twice as large, and divider can be AX, DX: AX, EDX: EAX or RAX RDX: respectively.
If the divisor has 8 bits, the result goes to and the rest in AH; If you have 16 bits, the result in AX and the rest in DX; If you have 32 bit, the result in EAX and the rest in EDX; If you have 64 bit, finally, the result goes in RAX and the rest in RDX.
The two statements cause an exception in two cases: If the divisor is 0 (because it makes no sense to divide by 0) and if the result is too large to fit in the destination register (overflow). All status flags are undefined after DIV or IDIV.
If you want to divide RAX to another 64-bit register (unsigned), make sure that the register RDX both at 0, otherwise called up the overflow (as well as unexpected results). If you make a sign with Division, we must extend the RAX in all bits of RDX, so build the dividend to 128 bits. This is done with the CQO (Convert to Octaword Quadword), which usually runs just before IDIV. Corresponding to 32, 16 and 8 bits are, respectively, CDQ (Convert to DWORD search: extends Quadword EAX into EDX: EAX), CWD (Convert Word to DWORD search: extends AX DX <: AX) and CBW (Convert Byte to Word: extends to AX). None of these statements changes the flags.
There is no form of Division for immediate, so if you need a fixed divisor, you must upload it on a log and then use it as a divisor.
Examples (assume that the divider is not equal to 0):
Logical instructions
Logical statements are those operating instructions bit; the most common are AND, OR, XOR, NOT, and shift rotations.
AND, OR, XOR
And, OR, and XOR (eXclusive OR) are binary operations (i.e. with two operands) that have the same syntax to ADD and SUB. This Act by making their operations between corresponding bits of their operands.
And sets to 1 in all and only those bits such that corresponding bits of both operands are 1.
Or sets to 1 in all and only those bits such that at least one of the corresponding bits of the other two operands is 1.
XOR the destination 1 imposed on all and only those bits such that corresponding bits of the other two operands are different.
Assuming that the initial values of two 8-bit registers, in binary, are 10110010 and 11100111; then:

These instructions are often used to manipulate individual bits: a clear all bits in the second operand are 0 and leave the others unchanged. a set to 1 OR all bits that are 1 in second operand and leave others unchanged. a XOR inverts all the bits that are 1 in second operand and leave others unchanged.
The XOR instruction is also commonly used to clear a log, by XORing the log and himself. However XOR has the side effect of changing the flags; in the rare case, rather, where it is necessary to preserve the flag, you can use a simple MOV, but has the flaw of having the longest encoding.
A useful property of the XOR operation is as follows: two XOR operations to cancel the same value (i.e. it is always true that a XOR b XOR b = a); This makes it suitable for simple encryption routines.
All these instructions set the flags SF, ZF and PF depending on the result, zero always OF and CF (for obvious reasons cannot generate report!), while the value of the AF is undefined.
Examples:
NOT
NOT education, unlike other logical operations, has only one operand, a register or memory value of 8, 16, 32 or 64 bits. This statement makes the 1 's complement of its operand, i.e. inverts all the bits. The change to the target registry is equivalent to one with an XOR value with all 1 bits; However, the statement does not change NOT no flags.
SHL, SHR, SAL, SAR
SHL and SHR instructions (SHift Left and SHift Right) make the shift operation of a value.
Shift consists in iterating through the specified number of bit positions. For example, if a log contains the binary value 01101101, shift to the left by one position is 11011010; the shift to the left by two positions is 10110100 (the first two bits are "pushed out", while the bottom two bits are filled with 0. Shift right by 1 bit is 00110110; the shift to the right by 2 bit is 00011011 (this time are pushed out the bits, and zeros are added from the left).
SHL and SHR has 2 operands; the first is a register or memory value (8, 16, 32 or 64 bits), and is the destination; the second operand can be register CL, or an immediate 8-bit unsigned (i.e. between 0 and 255), and represents the number of positions you want to shiftare the destination. The second operand are considered only the low order bits 5 (or 6 If the target has 64 bits), so that the counter of the number of positions between 0 and 31 (between 0 and 63 if the target has 64 bit).
SHL and SHR with a different counter from 0 change flags (the details can be seen in the manual); in particular, the CF is equal to the last bit that was pushed out.
Examples:
From the arithmetical point of view, a shift to the left by n bits is equivalent to multiplying an unsigned number for 2n; a shift to the right by n bits is equivalent to a Division (with truncation) of an unsigned number for 2n. The use of shift to avoid multiplications and divisions (mainly) is considerably more efficient. Obviously the shift you can use for other purposes bit manipulation
If you want to perform multiplication is division by powers of 2, signed numbers using the instructions SAL (Arithmetical Left Shift) and SAR (Aritmetical Right Shift). The syntax of operands is the same, and also the functions are similar. In fact, SAL is an alias of SHL and does not differ in anything (the opcode is only one, not two different instructions). SAR, instead, behaves as SHR, except that the bits that "come" from left are filled in with the value of the sign bit of the original operand. So while the shift to the right by one bit of 10011010 01001101 shift is arithmetic, is 11001101. Note that binary 10011010 equals decimal -102, while 11001101 is equal to -51 (half!).
The result of the SAR with no counter is equal to that of IDIV with 2n splitter only for positive numbers or when the Division is correct; in fact, while SAR truncates for defect, IDIV truncates toward 0 (so to excess in the case of negative numbers). For example, if you use IDIV to split -9 to 4, the result is -2 and the rest -1 (note that this is not consistent with the mathematical definition of the Division with remainder, where else is always positive). Using SAR for -9 shiftare instead of 2 bits, the result is -3 (and the rest, which in this case is not calculated, is 3).
ROL and ROR
The rotations are very similar to shift; the syntax of ROL (ROtate Left) and ROR (ROtate Right) is the same as SHL and SHR. The difference is that the bits "driven out" from a fall on the other side. With the same example as before, left rotation by a bit of 01101101 is 11011010. Right rotation is 10110110. In this case, the CF is set as the last bit pushed out.
Control instructions
CMP and testing
The CMP instruction (CoMPare) has exactly the same syntax of SUB. In fact also carries out the same operation, except for one detail: does not change the target log. The only effect is to update the status flags based on the result of the subtraction between the first and the second operand. Typically it is used to compare two numbers before a conditional jump statement (see below).
The TEST statement, similarly, has the same syntax and the same function AND education; in this case, without modifying the target log, but only changing the flags. You can use, for example, to see if some bits of a value is 1 or 0:
A classic use is to verify if a register that is 0 or not:
CMP and tests are useful especially with conditional jump instructions.
Data conversion instructions
MOVZX, MOVSX, MOVSXD
MOVZX instructions (MOVe with Zero eXtend), MOVSX (MOVe with Sign eXtend), MOVSD (MOVe with Sign eXtend DWORD search) are used to perform conversions to get smaller in larger data. All require two parameters, the first one (the target) is a register, the second (the source) a register or a memory value.
The first parameter of MOVZX and MOVSX can be 16, 32 or 64 bits, while the second can be 8 or 16 bit (but cannot be both 16 bit). MOVZX zero-extends the source and saves the result in the destination. MOVSX usa a sign-extension. Examples:
The MOVSXD statement exists only in x 64, and serves to extend (with sign) an entire 32 64 bit from to. The first operand is a 64-bit register, the second a register or a memory value to 32 bits. Example:
There is no instruction designed to make an unsigned extension. The most attentive will have already figured out why: just a simple MOV with 32-bit destination. In fact, x 64, operations on 32 bit registers are zero-extended automatically, it can make sense a statement (at first glance silly) like this:
Flow control statements
The flow-control statements are statements that allow you to change the Instruction Pointer, making a procedure call (CALL/RET), to jump (JMP) or a conditional jump (Jcc).
The flow control statements (except RET) take a parameter that is more frequent in cases of an address relative to RIP. This displacement can be large, up to 32 bit (with sign), so this form of addressing specifies distant destinations allows up to 2 GB from the current statement.
Assemblers, however, you take the load to calculate the correct displacement, allowing you to specify the destination through a symbolic name said label (label).
JMP
The JMP (JuMP) instruction performs an unconditional jump to the destination specified by the operand. In its most common form, the operand is an 8-bit displacement to (near jump) or 32 bits (short jump). Near and short jump allow jump only within the same segment; the far jump (which we don't care about), instead, allow you to jump to a destination of another segment.
In MASM and other assembler, obviously not you write directly to the displacement, but rather indicates the name of a label, leaving the task of coding to the assembler. For example, an infinite loop could have this structure:
no alternative, the operand of a JMP can be a log or a value in memory, that represents the target of the jump (which is the new value of rIP):
Or:
JCC
The family of Jcc instructions (Jump if condition) allows to perform branching, i.e. of jumps that are made if a condition is true, ignored otherwise. The condition is checking the State of one or more status flags. As JMP, Jcc also have only one operand, which can only be a relative displacement (therefore can only be short and near).
See the list of conditional jump instructions; in total there are 16 different instructions, but the mnemonics are more effective, because of the many synonyms:
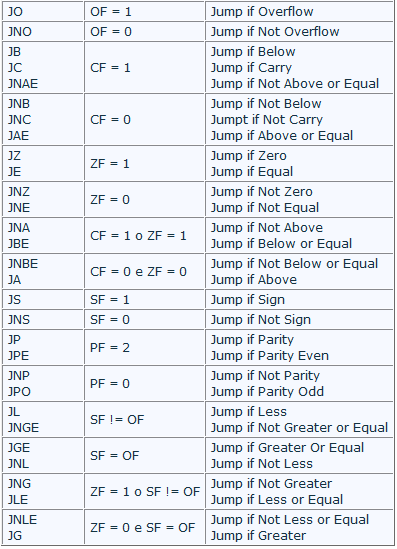
Were invented many synonyms to help you choose the most appropriate based on the meaning of the code, in order to improve the readability of source code. Of course the disassembler are not always the most consistent between aliases available, given that cannot understand the meaning of the code.
The names of many of these instructions make sense only if you are after a comparison statement (CMP or SUB, of course), while others specify only which control flags (for example JC, JO and JP).
It should be noted that the terms above/below/less and greater are not synonyms: above and below make sense after a comparison of unsigned integers, while greater and less sense after a signed integer comparison.
Let's see some examples:
With conditional jump instructions you can create all the high-level constructs.
A type code
Becomes something like (assuming rax and rbx are a and b):
A loop to repeat code 100 times you write usually as follows:
Of course you can translate into assembly language any high-level construct.
CALL and RET
The instructions CALL and RET (RETurn) are used to implement procedure calls.
Also for the CALL statement versions exist near and far; We will analyze just the first case.
The CALL stack puts the rIP (RIP in x 64, x 86 in EIP) of the next statement (it is called return address, return address). Then behaves similarly to the JMP instruction, jumping to the address specified by its single operand. In this case, the operand can be a 32-bit displacement of (i.e., for those who program a label), a record, or a value in memory.
The RET instruction allows you to continue executing the instruction following the CALL. RET pulls the return address off the stack and sets it as the new rIP.
RET may also have a parameter, an immediate 16-bit unsigned, which is added to the rSP after removing the return address stack. In fact, depending on the calling convention, the caller stack puts some or all the parameters required by the function call; the RET is involved then increase rSP to remove them.
Final Notes
Closes this thread here. I hope to be able to not make boring a subject which, by its nature, is inspiring and very creative and it is necessary to understand the workings of malware analysis tools such as Ollydbg.
Source
Intel documentation : http://www.intel.com/content/www/us/en/processors/architectures-software-developer-manuals.html
AMD documentation : https://en.wikipedia.org/wiki/X86-64#AMD64
Overview of x64 Calling Conventions : https://msdn.microsoft.com/en-us/library/ms235286.aspx
And : my school information over the next two years
Thanks everyone !!!
Introduction
Write the introduction is always the hardest part, because it always ends up that the reader becomes bored with things that already expects.
In this tutorial we will discuss assembly language. Have a great familiarity with this language is essential because, not having available sources of malware files that you want to analyze, the disassembler listing (or debugger) is the only thing you have.
For those who want to learn to program in assembly language, here you will find enough information to get an idea of how things work, but not so many that you can start writing code.
The tutorial is divided into two parts: in the first we will see the synthesis processor architecture; in the second, more substantial and can be used as a simple reference manual, we will analyze all statements.
Prerequisites
It would be nice if anyone could understand this tutorial, but you can't help but consider some prerequisite.
You need a good familiarity with the binary and hexadecimal numbering and changes from a base to the other; to those who had not familiar with these concepts suggest you return here after reading some tutorials about it.
Well, let's start now to analyze the AMD64 architecture (henceforth simply x 64). Let's start with the first part a bit more where we see no theoretical even a line of code; I promise that I will try to be brief. In the second part we will see all the basic instructions and ... the code will arrive.
Essay
x 86 and x 64
The x 64 architecture is essentially an extension of the previous Intel IA32 architecture, which is present in all PCs from the 80386. In the standard size IA32 operand was 32 bits (as in the past had been to 16 bit); x 64 architecture general purpose registers (and memory addresses) are 64 bits long.
The introduction of 64-bit processors, the AMD64 wasn't the only competitor in the game, since the Intel IA64 his proposed a completely different, but renounced the backward compatibility (i.e., compatibility with previous processors). As is known, in computer science, the sacredness of this principle cannot be put into question; the AMD64 has caught on and, now, even the Intel has made substantially its compatible processors (Intel and AMD's implementation has many names: EM64T, Intel 64, Intel IA32e).
From now on I'll use x 64 and x 86 names indicate, respectively, the AMD64, IA32. The term x 86-16 will be used for the 16-bit architecture of the intel processors prior to the IA32 (i.e. from Intel 8086 Intel 80286).
The bit and its multiples
Know all the equivalence 1 byte = 8 bits. Byte multiples more commonly used are as follows:
Word = 2 bytes = 16 bits
DWORD search (dword) = 2 word = 4 bytes = 32 bit
quadword (qdord) = 2 = 4 word dword = 8 bytes = 64 bits
More rarely you hear of oword (octaword), i.e. 2, also called double quadword quadword; sometimes fword (6 bytes) or even terabytes (ten bytes, 10 bytes).
Unsigned integers and sign
Integers can be of two types: unsigned (unsigned integers) or signed (signed integers). The size of integers can be 8, 16, 32, 64 bits; more rarely, 128 bit (in multiplication and Division in x 64).
An unsigned integer to n bits can represent all numbers between 0 and 2n-1. So an 8-bit unsigned integer that is at most 255, 16 bit is worth a maximum of 65535, to 32 bits over 4 billion, 64 bit more than 18 billion billion. The binary representation is usual, for which the largest number that can represent is that consisting of all bits 1.
A signed integer with n bits, instead, can represent all numbers between 2n and 2n-1-1-1. 8 bit so you go from -128 to +127, 16 bits from -32768 to +32767, to 32 bits from a smaller number of -2 billion to more than 2 billion, to 64 bits by a number less than -9 billion billion to more than 9 billion billion.
Signed integers using a representation known as 2 's complement. The representation of positive numbers (and zero) remains the same; However, since positive numbers are limited to half of the possible n bit values, all (and only) non-negative numbers have the most significant bit ("leftmost") equal to 0; the numbers with the most significant bit is 1, the negative numbers. The most significant bit is called, for this reason, sign bit. In whole to 8, 16, 32, 64 bit, the sign bit has 7 index, respectively, 15, 31, 63.
The binary representation of a negative number by 2 's complement is very easy to get: represent in binary the number negative-x, just write x, reverse all his bits, then add 1. For example, working with 8 bit, suppose we want to write -6. The binary representation of is 00000110 6 (write the initial zero bits to emphasise that we are using 8 bit). Inverting all the bits you get 11111001; adding 1 you get 11111010. This is the 8-bit binary representation of -6. We note an important property: adding 6 representations and -6 you get 100000000, which in decimal is equivalent to 256; This number has 9 bits, if we cut to 8 bits we get 0 (because the size of the processor's operations always has a fixed number of bits, the truncation is implied). The fact that the sum of two opposite numbers 0 face is crucial, and in this consists the usefulness of 2 's complement.
It is better to acquire a good familiarity with these concepts.
Zero-extension and sign-extension
Arithmetic operations between numbers represented by the same number of bits are usual manner; It happens, however, often having to perform between operands of different size. In this case, the smallest size operand must be converted (implicitly or explicitly) to the right size.
In the case of transactions between unsigned integers, this is trivial: simply prefix the number of smaller size a 0 bit as many need to get the right size: the representation of 6 to 8 bit is 00000110, 16 bits is 0000000000000110. This process is called zero-extension.
In the case of signed integers, however, this does not work. More precisely, it only works for positive numbers. But the -6 representation is 11111010, with zero-extension 0000000011111010 is obtained, i.e. 250 decimal: not exactly the same thing. The reason lies in the special meaning of the sign bit and operation of 2 's complement. The representation of a 16 bit -6 is 1111111111111010, i.e. the extending 8 bits with 1 instead of 0. In General, the extension of signed integers is done filling all the bits with values equal to the sign bit. This mechanism is called sign-extension.
The registers
Inside the CPU there are a large number of registers for different functions. A log is only a memory cell, the fastest in the processor. They are used to store the State of the processor, continually modified as a result of execution of instructions.
Let's see first how is composed the register set of the x 86 architecture, and then see how it was extended in x 64.
X 86 registers
A first group of records consists of General Purpose Registers (GPRs), i.e. the General purpose registers, called so because, ideally, can be used for any purpose.
The General format of a general purpose register (let's take as example EAX) is as follows:
The lines should imagine how overlapping: the entire register is EAX, 16 bits ("right" in the numeric representation) form AX, the 8 bits forming AL (the letter L stands for Low). The 8 most significant bits of AX form the AH register (where H stands for High).
There are 8 32 bit registers for general use: EAX, EBX, ECX, EDX, ESI, EDI, EBP, ESP. The namespace and was added with the introduction of the IA32 architecture as an extension of earlier than 16 bits.
Often it is used to indicate all logs in uppercase or all lowercase, while eAX notation with the first letter indicates either AX or EAX. Similarly, using the notations eBX, eCX, and so on.
EBX, ECX and EDX have the same format as seen above, little EAX so subregister of EBX are BX, BH, BL, ECX are CX, CH, CL, EDX, finally, DX, DH, DL.
Normally each of these logs can be used for any purpose, although there are a number of exceptions: we will analyse later. The register EAX is also called accumulator, more for historical reasons which, although there are a number of situations where its use is necessary and others where it is preferable to other registers. To a lesser extent, this is also true for EBX, ECX, EDX.
For other General Purpose registers in 32 bit (ESI, EDI, EBP, ESP) you cannot access subregister of 8 bits, while the subregister of 16 bits are, in order, Yes,, BP, SP.
ESI and EDI (whose acronyms are for Source and Destination Index Index) can be used for any purpose as the previous ones, but have a special support for use as indexes for operations on strings (scanning, copying, comparison). The respective subregister to 16 bits are THERE and, while there are subregister in 8 bits (as already pointed out).
EBP and ESP (Base Pointer and Stack Pointer) are used in the management of the stack (we'll delve into later). ESP indicates the current location onto the stack, while the base usually tip EBP stack, i.e., for instance, the area of memory where the local data of a function (normal procedure variables, not visible outside). Actually nothing prohibits using EBP for other purposes, but this is not very common. The counterpart to 16 bits are BP and SP.
Ultimately, the set of General Purpose Registers x 86 architecture provides:
8-byte registers (AH, AL, BH, BL, CH, CL, DH, DL);
8 a word records (AX, BX, CX, DX, IT, BP, SP);
8 1 dword registers (EAX, EBX, ECX, EDX, ESI, EDI, EBP, ESP).
A part is register EIP (with the IP subregister), the Instruction Pointer: it always points to the next instruction to be executed. EIP you can't read or write as other registries, but can be changed indirectly or with flow control statements that we will see below.
A very important log is the EFLAGS register. This log is a bit field, consisting of a large number of flags, values binary (0 or 1) with disparate purposes. Here's a diagram:
| | | 29 30 31 | 28 | | | 25 26 27 | | | 22 23 24 | 21 | | | 18 19 20 | 17 | | 16 15 14 13 12 | | | | 10 | 11 09 | | | 07 08 06 | 04 03 05 | | | | | 00 01 02 |
Apart from a number of flags, in fact, useful only for system programming, there are 6 (the status flags) that are set to 1 or 0 depending on the outcome of many instructions. It is essential to know.
Carry Flag (CF, bit 0)-carry Flag. Is put to 1 when there is a carry (in the case of a sum) or a loan (for subtraction) from the most significant bit of an operation. For example, EAX contains the hexadecimal value 0x9000000 and execute the instruction ADD EAX, EAX, the result (0x120000000) is truncated to 32 bits (0x20000000), and the presence of carryover is signalled by setting the Carry Flag to 1. Shift operations or, instead, the meaning is different, but we will see later.
Parity Flag (PF, bit 2)-parity Flag. Is set when the least significant byte of the result of many operations contains an even number of 1 bits. Is commonly used in data transmission systems such as control system; for anyone who is a novice may be sufficient to know existed. Actual use is quite rare.
Auxiliary Carry Flag (AF, bit 4)-is set to 1 when there is a carry or borrow a bit from the third operation of type BCD (Binary Coded Decimal), zero otherwise.
Zero Flag (ZF, 6 bits)-is set to 1 if the result of an operation is zero, otherwise it is cleared.
Sign Flag (SF, bit 7)-sign Flag. Is put to 1 if, after an arithmetic operation, the most significant bit (the sign bit) is 1. Otherwise it is cleared.
Overflow Flag (OF, bit 11)-is put to 1 when the result of an operation is too large (overflow) or too small (underflow) to be contained in the register of destination; is set to zero otherwise. More specifically, it is set to 1 if the sign bit (most significant) of the result is different from that of both operands. In the case of sums or subtractions is easy to be convinced that this condition is equivalent to an overflow/underflow.
The importance of status flags will be clear when we will analyze the flow control statements (but are useful for other instructions).
Another noteworthy flag (classified as control flag, since it alters the behavior of the processor) is the Direction Flag (DF, 10 bits). It allows you to decide the direction in which they are carried out on string operations, i.e. If the eSI and eDI registers are incremented or decremented at each repetition. Operations on strings will not be treated.
Special registers for memory management are the Segment Registers, 16-bit registers containing a segment selector. The segments allow you to manage segmented memory models (...), which were typically used multiprocessing systems to isolate each from other process transparently. They are CS (Code Segment), DS (Data Segment), ES (Extra Segment), FS, GS, SS (Stack Segment). The Code Segment is the segment containing the code, while others are for data segments; DS is the default for most (others to be used, must usually be indicated explicitly in assembler, which will encode them properly in the machine code). SS is the segment that contains the stack. FS and GS segments are more data whose names have no special meaning and should only continue the alphabetic sequence; were introduced in Intel 80386 processors.
Other registers used for advanced uses are the Debug Registers (DR0, DR1, DR2, DR3, DR6 and DR7), mainly used by debugger, and the Control Registers (CR0 at CR4), used only at the level of the operating system and by normal application ever.
X 64 registers
The AMD64 architecture is an extension of the IA32 designed to maintain backwards compatibility. X 64 processors can run in 32 bit applications in 64-bit operating systems, but may even act like 32-bit processors (and then run a 32-bit operating system). However, to really leverage the power of x 64 architecture is necessary to compile programs specifically for this architecture and own a 64-bit operating system, so that the processor can run at 64 bits.
In 64-bit mode, the x 64 processors provide a series of extensions.
All General Purpose Registers, the Instruction Pointer, the flags are large 64 bit instead of 32.
8 GPRs are added, for a total of 16. The lack of registers was one of the main reasons to rethink the architecture from x 86 to x 64.
The registers RAX, RBX become, RCX, RDX, RSI, RDI, RBP, RSP. The extended registers 8 are simply numbered from R8 to R15. For each register can also be accessed at sottoregistri by 32-, 16-, 8-bit content in the less significant. From RAX to RSP names are those already seen (e.g. EAX, AX, AL), but they become even addressable 8 bits of RSI, RDI, RBP, RSP, with SIL, DIL, BPL, SPL respectively. The subregister to 32, 16, 8-bit registers R8 to R15 themselves by adding the suffixes D, W, B respectively, which are of course for Dword, Word, and Byte. For example the subregister to 16 bits of R8 is called R8W.
You can still access the register AH, BH, CH and DH, but you cannot mix in a single statement these logs with extended ones (i.e. those that do not exist in the x 86 architecture).
Schematically, the GPRs becomes:
16 64-bit registers: RAX, RBX, RCX, RDX, RBP, RSI, RDI, RSP, R8, R9, R10, R11, R12, R13, R14, R15;
16 32-bit registers: EAX, EBX, ECX, EDX, EBP, ESI, EDI, ESP, R9D, R10D, R8D, R11D,, R13D, R12D, R14D R15D;
16 16-bit registers: AX, BX, CX, DX, BP, SI, to, R8W, R9W, SP, R10W, R11W, R12W, R13W, R14W, R15W;
formed from 8 registers 16 bits: logs, BL, CL, DL, BPL, DIL, SIL, R8B, R9B, SPL, R10B, R11B, R12B, R13B, R14B, R15B;
4 8-bit registers in the most significant bits of AX, BX, CX, and DX, namely: AH, BH, CH, DH.
The EIP register was extended in RIP, the EFLAGS register and extended in RFLAGS.
Unlike the x 86, x 64 architecture provides the ability to use RIP for addressing, i.e. to read or write to memory locations that are RIP up to 2 GB. We will see later on the details of addressing related to RIP.
RAX notation is often used to denote indifferently, EAX or RAX AX; similar notations exist for all other registers.
Segment registers are hardly used anymore in 64-bit mode, since the memory management using segmentation becomes superfluous if the pointer size is 64 bits (which means one address space of 264 bytes, i.e. really many). Are considered only the registers CS, FS and GS, but much less essential than in x 86. The other Segment Registers are simply ignored.
32-bit operations on x 64
In x 64, the default size of the operands is, for the most part, 32-bit instructions. Machine language encodings of the 64-bit versions of the instructions require the addition of a special prefix instruction encoding; This prefix enables access to the extended set of registers.
Unlike the subregister operations to 8 and 16 bit, acting only on the subregister leaving unchanged the other 56 48 bit, or changes to the 32-bit registers reset the 32 most significant bits of the register (in technical jargon, are zero-extended). For example, assuming that the initial state is the following:
Code:
RAX = 0002_0001_8000_2201
RBX = 0002_0002_0123_3301Assuming the variants to 64, 32, 16 and 8 bit (the statement that adds the second operand to the first, saving the result in the first), you have the following options:
Code:
ADD RBX, RAX Result: RBX = 0004_0003_8123_5502
ADD EBX, EAX Result: RBX = 0000_0000_8123_5502
ADD BX, AX Result: RBX = 0002_0002_0123_5502
ADD BL, AL Result: RBX = 0002_0002_0123_3302The second line is highlighted to emphasize the different behaviour of the 32-bit version than the other.
Memory
From the application viewpoint, the memory can be viewed as simply a set of contiguous bytes, each with its own address, which you can read or write. In fact, an address contained in a pointer is a virtual address (virtual address) that must go through phases of translation to get the physical address (physical address), i.e. the real address in memory. The translation takes place transparently to applications.
Segmentation
In models that use memory segmentation, each memory access (explicitly or implicitly) also a segment selector (contained in a Segment Register), used by the hardware to know where in memory segment (basis), how big is (limit) and the type of access allowed. Where access is outside the segment size or be of a type that is not allowed (e.g. writing a read-only segment), the hardware raises an exception to signal the abnormality (that, if not handled properly, causing the crash, i.e. the closure enforced by the operating system).
The segmentation was very common in older systems, but is almost out of use in modern x 86 systems, which use a flat memory model, with having segments 0 and base limit 4 GB, which is essentially disabling the segmentation; for this reason has been almost completely removed from the x 64 architecture.
Paging
Paging, instead, provides a protection system more homogenous, allowing you to specify the permissions for each page, i.e. a large block of memory, usually 4 kb (4096 bytes). It also allows you to remap any way physical memory that the application addresses consecutive believes (in the only place that knows, that virtual) can be in any position in RAM or, indeed, can be removed and stored in the hard drive to make room for something else, and will be in RAM when the application wants to access it again (thanks to modern operating systems paging can "emulate" more RAM than is actually there , albeit with a performance degradation). Everything happens transparently to the application.
Order of bytes
In the case of dimension data a byte (or composite data as ASCII strings, which are simply arrays of bytes) there is only one possible order in memory: each byte has its unique position.
However, in the case of dimension data word (2 bytes), dword (4 bytes) or qword (8 bytes) there are two main conventions: big-endian and little-endian.
In big-endian Convention, are written by more bytes significant to least significant, so that their simple concatenation form as complete. For example, if memory address 0x402000 is the dword, 0x11223344 memory were, in order, the bytes 0x11 (at 0x402000), 0x22 (at 0x402001), 0x33 (at 0x402002), 0x44 (at 0x402003). Big-endian notation is the standard for communication over the network, but is also used in some processors.
In little-endian Convention, instead of multiple bytes of the byte are written from most significant to least significant, i.e. in reverse order in memory. The 0x11223344 dword at 0x402000 would be stored as follows: 0x44 (at 0x402000), 0x33 (at 0x402001), 0x22 (at 0x402002), 0x11 (at 0x402003).
All x 86 and x 64 processors use little-endian Convention, so you have to get used to the bytes reversed.
An undoubted advantage of little-endian notation is this: the same data is represented and simultaneously correctly under different sizes. For example, the 0x00000055 dword at 0x402000 becomes: 00 00 00 55. Reading the word at the same address reads: 00 55, i.e. 0x0055 on little-endian; reading a byte 0x55 reads. This can be very convenient for those who program in assembly.
Some processor has also adopted more complicated notations (mixed-endian).
Stack
The stack is a region of memory available for each process to save temporary information.
A stack is a LIFO data structure (Last-In first-out), i.e. a structure in which information is removed in reverse order compared to that. The pointer to the last item pushed onto the stack is contained in the rSP register (i.e. in RSP if we x 64, x 86, ESP in SP in the old x 86-16). Segmented memory models in x 86, it is useful to know that the stack is contained in SS and that all references that contain rBP or rSP are made by default through the SS.
The stack can be used to store data in a register to be used later, in order to free the log for other purposes. The LIFO structure, the data is restored in the reverse order than how they were entered. If I saved, in order, RAX, RSI and R14, then restore first R14, CSR and then finally RAX. We will see later PUSH and POP instructions that are used to manipulate the stack.
Another stack function is to manage the flow control in procedure calls. When a procedure is called, in fact, you must save the address of the instruction from which to restart execution at the end of the procedure. This return address (return address) is implicitly saved on the stack from the CALL statement to call a procedure, and is removed from the RET statement that is always the last of a procedure.
The parameters passed to a procedure are sometimes placed on the stack by the caller (sometimes are, instead, passed through the logs ... just agree!). Finally, is that stack is reserved space for the local variables in a procedure (those that exist only during the execution of the procedure itself and cease to exist upon its completion).
We will return later to talk more in detail of stack, PUSH and POP instructions, flow-control statements and calling conventions.
The assembly language
Let's finally talk of assembly language.
The syntax that is used in this tutorial is the MASM assembler; However, it is not difficult to adapt the syntax to other assemblers, in which case please refer to the respective manuals to know the differences.
Basic syntax
The syntax of assembly instructions is in general very simple. Each statement has a name that is mnemonic because basically said just need to remember not the binary encoding in machine language. The numeric code that represents the statement has said opcode (operation code contraction).
Each statement can have 0, 1 or 2 operands; in rare cases 3. The complete statement, in a separate line in the source file, is formed by the mnemonic and the list of its operands. Between the mnemonic and the operand list, of course, it takes at least one space; operands are separated by commas. For example the ADD statement has two parameters, which (among other things) can be two registers. A statement is valid:
Code:
add rax, rbxThis sum statement register rbx, rax register saving the result in rax. We can already highlight a constant of all statements with two operands: if it makes sense to talk about source and destination (i.e. the operand in which the processor saves the result), the MASM syntax requires that the destination is always the first operand (assemblers exist that use the AT&T syntax with the operands reversed; they are more used in Linux environment). So many instructions will be of the type:
mnemonic dst, src
The number and type of its operands are specified in detail in the manuals (see bibliography), but for all the basic instructions we will see them later.
Types of operands and synopsis
The instructions may require different types of operands. The main ones are the following: a register, a value in memory, an immediate (i.e. a numeric constant) or relative (i.e. going in all the Instruction Pointer).
The operands may be of different sizes, so afterwards, when we describe the synopsis of the instructions always specify what are those allowed.
Let's start with some general remarks on the assembly and on the format of the instructions; This section continues with a long introduction to assembly instructions: we will analyse, with a certain degree of detail, some forty assembly instructions: a relatively small subset compared to the hundreds of existing instructions, but that covers almost all the instructions that you will encounter in practice.
Don't worry about memorizing everything immediately, is not required; This is possible (and actually quite easy) only with practice. But don't be in a hurry to go to the next section.
Size of operands in memory
Operands in memory, are indicated in MASM, but also in the many listing disassembler, enclosed in square brackets. For example, the instruction MOV RAX, [RBX] copy in RAX the qword contained the memory address pointed to by RBX. We observe that the second operand contains no information about size; However, in the MOV the two operands have the same size, and the size must be the same, i.e. 64-bit RAX. In other cases, however, there would be ambiguity; for example education INC. [RBX], which increases the value pointed to by EBX, exist in 8, 16, 32, 64 bits. In this case, both x 86 x 64 that the default size is 32 bits. To indicate a size other than the default, it prepends an associative expression as "byte", "word ptr ptr, dword ptr" "" or "qword ptr". For example INC. bytes ptr [ebx] increments the byte pointed to by qword ptr INC ebx, [ebx] increments a qword, and so on.
The General addressing format an operand in memory (i.e. What can be contained in square brackets) on x 86 is as follows:
base + index * scale + displacement
Where base and index are two 32-bit registers (but cannot be ESP index), the scale factor may be 1, 2, 4 or 8 (if 1 is obviously not shown), the displacement is an integer with the score at 8, 16 or 32 bits. For example,:
mov rdx, qword ptr [ebx + ecx * 8 + 24]
In x 64 you can use the same type of addressing, index-based, stairs and displacement; base and index are usually general purpose registers any to 64 bits, but you can also use 32-bit registers (but not one to 64 and 32 bit, of course), in which case you can address only part of the address space (4 GB). The displacement is a signed integer of 32 bits, so it is no longer possible to type a mov eax, [address] where address is an absolute address in memory.
x 64 introduces a form of addressing not present on x 86: addressing related to RIP (in Italian is not that great, English speakers say RIP relative addressing). In this case, you have only a displacement of 32 bits the processor adds to RIP the next statement. In this way you can address data which are up to 2 GB RIP, which is usually enough for normal applications (an executable image fails virtually never this size!). An advantage of this form of addressing is to make the code independent of its actual location in memory, while with absolute addresses a possible relocation (i.e. uploading to an address other than the one provided) requires the correct loader absolute addresses (although, in reality, this operation has never been particularly expensive).
Data alignment
In-memory data should always be aligned. A data is properly aligned when its in-memory address is a multiple of its size (I refer here solely to data whose size is a power of 2). So for a b there are never problems, but a word should be in an address divisible by 2 (i.e. the last bit 0), a dword in an address divisible by 4 (the last two bits are 0), a qword an address divisible by 8 (last three 0 bits), and so on.
Why is convenient to align the data is the gain in efficiency: so the processor accesses them more quickly. Access to a dword is not aligned, for example, requires the processor to make two requests to memory instead of one.
In 64-bit Windows, however, the alignment is required stack API calls, so it becomes more than a mere performance issue.
The MOV instruction
The MOV instruction is one of the main and most common assembly instructions. The General format is:
Code:
MOV dst, srcand what education does is copy in dst data that are contained in the src. The two operands are not necessarily the same size.
In its simplest form, dst and src are registers or records and an operand in memory (but not two operands in memory):
Code:
mov rcx, r12 ;copy r12 in rcx
mov rcx, qword ptr[esp] ;copy in rcx the qword at stack top
mov byte ptr[rsi], r12b ;copy the byte less significant of r12
;to the address pointed to by rsiIf dst is a register to 8, 16, 32 or 64 bit, src may also be an immediate of the same size. If dst is an operand in memory of 8, 16, 32 bit, src can be an instant of the same size, while if dst is an operand in memory to 64 bit, src may still be an immediate 32-bit signed that is extended with the sign (sign-extended) to 64 bit and copied to dst.
Code:
mov al, 12h ;write 8 bit number in al
mov si, 1234h ;write 16 bit number in si
mov ecx, 11223344h ;write 32 bit number in ecx
;(and resets the most significant 32 bits of the rcx!)
mov r14, 1122334455667788h ;write in r14 a 64 bit number
mov byte ptr[ebp], 64h ;Initializes a byte in memory
mov word ptr[ebp], 12345 ;Initializes a word in memory
mov dword ptr[ebp], 401000h ; Initializes a dword in memory
mov qword ptr[ebp], -5 ; Initializes a qword in memory
;with a full 32 bit signed
mov qword ptr[ebp], 100000000h ;WRONG! the secon operand
;cannot be interpreted as
;a signed integer to 32 bit!If dst is AL, AX, EAX or RAX, you can also read a memory value at a given address to 64 bits (of course, you can do only x 86 with a 32-bit address). Mov is the only statement that can have a value as an operand in memory with an address to 64 bits.
Code:
mov al, byte ptr[1122334455667788h] ;read a byte in memory
mov rax, qword ptr[1122334455667788h] ;read a qword in memory
mov rbx, qword ptr[1122334455667788h] ;WRONG!Of course, in practice it happens very rarely write the address in this way, since you can use the RIP-relative addressing. In x 86, however, this is quite common for accessing global data.
Conversely, if src is AL, AX, EAX or RAX, dst can be a value in memory that is given the address (example: mov byte ptr [1122334455667788h], al).
There are also variants of the MOV instruction to read or write the Segment Registers, Debug Registers or Control Registers.
The MOV instruction does not change the RFLAGS log.
PUSH and POP instructions
Push and POP are the two main instructions to manipulate the stack. Both take a parameter; PUSH to insert something in the stack, POP to pop it.
The PUSH decrements rSP register to a value of 8 in x 64, 4 in x 86; then save the value of the operand to the address pointed to by rSP. The operand can be either a PUSH registry, a value in memory or immediate. In x 64, the immediate cannot be 64 bit, but may be a signed integer to 32 bit which is sign-extended and put onto the stack as 64-bit value.
Code:
push rdx ;save RDX to stack
push qword ptr[rax] ;save to stack the value pointed by eax
push 12 ;save to stack the value 12 (the immediate is 8 bit, but
;the value pushed on the stack has 64 bit)
push 12345678h ;save to stack the qword 0x0000000012345678The PUSH with 32 bit working is the rule on x 86, but does not exist in x 64. Exists in both PUSH education architectures with working at 16 bit, but usually has little sense because it leaves the stack unaligned (but, for example, nothing prevents to use 16-bit 4 to PUSH and withdraw later one qword).
The POP instruction operand is a register or a location in memory of 16, 32 or 64-bit (32-bit version does not exist in x 64 x 86; instead, there is obviously the 64-bit version).
POP copies the value onto the stack in the destination operand, and then increments the rSP (8, 4 or 2 for POP to 64, 32, 16 bit).
Code:
pop rax ;save to rax the value at stack top
pop qword ptr[rdi] ;save to [rdi] the value at stack topThe beginners are often confused by the fact that PUSH (= put something stack) decrements rSP, while POP (= take away something from the stack) the increments. The stack grows backwards, so it's good to get used to.
Push and POP are often used, to save one or more values on the stack and restore them later:
Code:
push rbx ;save rbx
push rsi ;save rsi
push rdi ;save rdi
;...
;[code that use rbx, rsi and rdi]
;...
pop rdi ;save rdi
pop rsi ;save rsi
pop rbx ;save rbxNote that the order of POP is back than PUSH.
The PUSH is also used to pass parameters to a function call, when they are not passed through the logs (we will see later calling conventions).
To delete one or more elements from the stack without reading them, you can simply use the ADD instruction (add 8 * n bytes for RSP in x 64 is equivalent to removing n elements).
LEA
The LEA instruction (Load Effective Address) is connected, in a way, to the MOV. LEA takes two parameters, the first is a record to 16, 32 or 64 bits. The second is a value in memory.
In fact, the operand is in memory only, since, in fact, there is no access to the RAM of the processor. LEA in the copy destination only operand address in memory. (example)
Code:
lea rax, [rbx + rcx] ;puts in rax the sum of rbx and rcx
lea rbx, [label] ;puts in rbx the label address (in x64, it
;will be encoded via RIP-relative addressing)
;this stat. is 5 bytes, while
;l'equivalent whit MOV it is 9.
lea edx, [edx + edx*8] ;multiply by 9 edxThe last example shows the use of LEA to make simple calculations that, Alternatively, would require more than one statement. LEA also has the desirable properties, sometimes, do not change any of the flags.
In fact, the first operand and size the size of the registers used in addressing the second operand may be different. If the first operand is smaller, the result is truncated; If it is larger, is zero-extended:
Code:
lea ax, [rbx + rdi] ;puts in ax the 16 bit less of rbx+rdi
lea rbx, [eax + ecx*2 + 15] ;XCHG
The XCHG instruction (eXCHanGe) requires two operands, which can either be two registers, or a register and an operand in memory. The two operands can be great 8, 16, 32 or 64 bit, but must have the same size. The XCHG instruction swaps the values of the two operands.
Code:
xchg rax, rdx ;swap rax and rdx
xchg cl, byte ptr[rax] ;swap cl whit the rax pointed byte
xchg ecx, 12 ;WRONG! No operand can be an immediate!NOP
The instruction NOP (No OPeration) is the simplest that there is ... In fact, his job is to do absolutely nothing (apart, obviously, increase rIP to pass to the next statement!). The opcode 0x90 the NOP instruction is one byte; This makes it particularly useful for reverse engineering purposes . To counteract a statement (such as a conditional jump statement) you can replace it with a series of longtime NOP exactly how the statement (delete the instruction, in fact, would compromise the file alignment).
Mathematical statements
ADD and SUB
ADD and SUB instructions allow you to perform addition and sums. The General format is:
Code:
ADD dst, src ;add src to dst, saving the result to dst
SUB dst, src ;subtracts src to dst, saving the result dstwhere dst can be a log or a value in memory, src records, a value in memory or an immediate large signed up to 32 bits (the limit also applies if dst is great 64 bit). src and dst, however, cannot be both operands in memory, and must be the same size (except the case where src is an immediate, in which case, if it is smaller, it simply extended with the sign to be added/subtracted to dst). Examples:
Code:
add rax, rbx ;add rbx to rax
add ecx, eax ;add eax to ecx (and reset the high 32 bit of rcx!)
sub sp, word ptr [r12] ;subtracts the word in [r12w] to sp
sub al, ah ;subtracts ah from al
add dx, 1234h ;add to dx a 16 bit value
sub rbp, -5 ;subtracts -5 to rbp
add qword ptr [rax], -100000 ;add -100000 to qword in [rax]
add rsi, -3000000000 ;WRONG! The immediate is not 32 bitIf the second operand is immediate, both statements have shorter encodings if the target is AL, AX, EAX or RAX.
Both the ADD statement that the SUB statement change all the status flags 6 in a concorde to the result of the operation.
Sometimes the SUB statement is used to clear a log by removing himself, but for this purpose it is recommended (and more common) the logical XOR instruction.
NEG
The NEG instruction (Denied) has only one operand, a register or memory value to 8, 16, 32 or 64 bits; NEG make the 2 's complement of its operand, i.e. calculates the opposite. Of course it only makes sense for signed integers.
Code:
neg rax ;computes the inverse of rax
neg qword ptr[rsp] ;computes the inverse of qword pointed by rsp
neg r13b ;computes the inverse of the least significant byte of r13NEG sets the Carry Flag to 0 if the value of the operand is 0, otherwise sets it to 1. Other status flags (OF, SF, ZF, AF and PF) are set according to the result.
ADC and SBB
The instructions and SBB ADC (ADd with Carry respectively and SuBtract with Borrow) have the same syntax to ADD and SUB, but also the same function. The only difference is that ADC adds 1 to the result further if the Carry Flag is 1; Similarly, SBB subtracts 1 if the CF is 1. Instead behave exactly like ADD and SUB If CF is 0.
Instructions ADC and SBB serve to take account of the carry (carry) or loan (borrow) in the case of additions or subtractions in several parts. For example, if you want to add RAX: RBX (i.e. the concatenation of RAX, RBX and a 128-bit number) with RCX: RDX, you can use the following code:
Code:
add rbx, rdx ;sum the lower 32 bit
adc rax, rcx ;sum the above 32 bit, plus any carry overFor subtraction, instead:
Code:
sub rbx, rdx ;subtracts the lower 32 bit
sbb rax, rcx ;subtracts the upper 32 bitInc and DEC
Inc and DEC (INCrement and DECrement) have only one operand, which can be either a register or a memory operand. The effect of these instructions is to add (INC) or subtract (DEC) 1 to the operand, such as ADD and SUB instructions where the second operand is 1. Have a shorter encoding.
The only difference is that ADD and SUB keys INC and DEC preserve the Carry Flag; all other flags are changed in the same way.
MUL and IMUL
The MUL and IMUL instruction (MULtiply) are used to perform the multiplications, or unsigned integers.
The MUL instruction has only one operand, a register or memory value to 8, 16, 32 or 64 bits. Depending on the size of the operand, MUL performs the product between its operand, and a value of AL, AX, EAX or RAX, respectively; the result is saved in AX, DX: AX, EDX: EAX, RDX: RAX, where the notation with colons indicates concatenation. Target logs have a double size because, in General, the product of two n-bit numbers need 2n bits to be entirely content. Examples:
Code:
mul bh ;calculates al*bh, save the result in ax
mul r15w ;calculates ax*r15w, result in dx:ax
mul dword ptr[r12] ;calulates eax*[r12], result in edx:eax
mul rax ;calculates the square in rax, result in rdx:rax
mul 12 ;WRONG! The operand may not be immediate.The IMUL instruction is more flexible, and can occur with one, two or three operands.
In form to an operand (register or memory value to 8, 16, 32 or 64 bit), multiplies the loperando IMUL value of AL, AX, EAX or RAX (depending on the size of the operand) and save the result in AX, DX: AX, EDX: EAX or RAX RDX:; in other words, it works as MUL, except that multiplication is done considering the operands as signed integers. Example:
Code:
mul rbx ;multiply rax to rbx, result in rdx: raxIn form to two operands, the first is the destination, a register to 16, 32 or 64 bits, and the second a register or memory value of equal size, or an immediate value (if the smaller immediate operands, is sign-extended; if the operands are of 64 bit, the immediate is at most 32-bit anyway). In this case the target is multiplied by the second operand and the result is saved in the destination.
Code:
imul cx, r15w ;multiply cx to r15w
imul rdx, qword ptr[rsp] ;multiply rdx to [rsp]
imul bp, 10 ;multiply bp tp 10
imul rax, 123456789h ;WRONG! Immediate too large for 32 bitIn form three operands, the first is the destination, a register to 16, 32 or 64 bits; the second is a register or memory value of equal size; the third is an immediate (again, if the 8-bit immediate operands are larger, the immediate is sign-extended; are not allowed immediate 64 bit). The statement then multiplies second and third operand, and stores the result in the first.
Code:
imul rbx, rax, -99 ;calculates rax*(-99) and save the result in rbxWe observe that in two and three operands, the destination is not bigger, so if the result is too large to fit in the destination, you would get only half less significant.
In the case of MUL or IMUL with an operand, the Carry Flag, Overflow Flag and are put to 1 if half of the result is different from 0, and are set to zero otherwise. For shapes in two and three operands of IMUL, CF and OF are 1 in case of overflow, i.e. If the result is larger than the destination register (in fact not much different from the case at 1 operand).
Other flags status (SF, ZF, AF and PF) are undefined after MUL, IMUL or so you should not rely on their value.
Div and IDIV; CBW, CWD, CDQ, CQO
DIV and IDIV instructions perform the divisions, respectively without and with mark. Both statements take a single operand, a register or memory value to 8, 16, 32 or 64 bits that represents the divisor. The dividend is twice as large, and divider can be AX, DX: AX, EDX: EAX or RAX RDX: respectively.
If the divisor has 8 bits, the result goes to and the rest in AH; If you have 16 bits, the result in AX and the rest in DX; If you have 32 bit, the result in EAX and the rest in EDX; If you have 64 bit, finally, the result goes in RAX and the rest in RDX.
The two statements cause an exception in two cases: If the divisor is 0 (because it makes no sense to divide by 0) and if the result is too large to fit in the destination register (overflow). All status flags are undefined after DIV or IDIV.
If you want to divide RAX to another 64-bit register (unsigned), make sure that the register RDX both at 0, otherwise called up the overflow (as well as unexpected results). If you make a sign with Division, we must extend the RAX in all bits of RDX, so build the dividend to 128 bits. This is done with the CQO (Convert to Octaword Quadword), which usually runs just before IDIV. Corresponding to 32, 16 and 8 bits are, respectively, CDQ (Convert to DWORD search: extends Quadword EAX into EDX: EAX), CWD (Convert Word to DWORD search: extends AX DX <: AX) and CBW (Convert Byte to Word: extends to AX). None of these statements changes the flags.
There is no form of Division for immediate, so if you need a fixed divisor, you must upload it on a log and then use it as a divisor.
Examples (assume that the divider is not equal to 0):
Code:
xor rdx, rdx ;reset rdx
mov ebx, 10 ;put 10 to rbx
div rbx ;divide by eax per 10
;result will be in rax, the rest in rdx
cdq ;extends the sign of EAX in EDX: EAX
idiv dword ptr[r13] ;divide EDX:EAX by the dword pointed to r13Logical instructions
Logical statements are those operating instructions bit; the most common are AND, OR, XOR, NOT, and shift rotations.
AND, OR, XOR
And, OR, and XOR (eXclusive OR) are binary operations (i.e. with two operands) that have the same syntax to ADD and SUB. This Act by making their operations between corresponding bits of their operands.
And sets to 1 in all and only those bits such that corresponding bits of both operands are 1.
Or sets to 1 in all and only those bits such that at least one of the corresponding bits of the other two operands is 1.
XOR the destination 1 imposed on all and only those bits such that corresponding bits of the other two operands are different.
Assuming that the initial values of two 8-bit registers, in binary, are 10110010 and 11100111; then:
These instructions are often used to manipulate individual bits: a clear all bits in the second operand are 0 and leave the others unchanged. a set to 1 OR all bits that are 1 in second operand and leave others unchanged. a XOR inverts all the bits that are 1 in second operand and leave others unchanged.
The XOR instruction is also commonly used to clear a log, by XORing the log and himself. However XOR has the side effect of changing the flags; in the rare case, rather, where it is necessary to preserve the flag, you can use a simple MOV, but has the flaw of having the longest encoding.
A useful property of the XOR operation is as follows: two XOR operations to cancel the same value (i.e. it is always true that a XOR b XOR b = a); This makes it suitable for simple encryption routines.
All these instructions set the flags SF, ZF and PF depending on the result, zero always OF and CF (for obvious reasons cannot generate report!), while the value of the AF is undefined.
Examples:
Code:
and rax, rbx
and al, 11111011b ;reset the antepenult bit of al
or rax, 16 ;16 in binary is 10000, then set the fifth from last bit
xor bx, -1 ;-1 ha tutti i bit 1, then inverts all the bit of bx
or ecx, dword ptr[rbp]
xor al, r8b
xor edx, edx ;reset edx (in x64 reset anyway all rdx)
and r15, 102030405h ;WRONG! The immediate is too big!NOT
NOT education, unlike other logical operations, has only one operand, a register or memory value of 8, 16, 32 or 64 bits. This statement makes the 1 's complement of its operand, i.e. inverts all the bits. The change to the target registry is equivalent to one with an XOR value with all 1 bits; However, the statement does not change NOT no flags.
Code:
not rdx
not dword ptr[rax*4 + rsi]
not 15 ;WRONG! Obviously the operand cannot be immediate!SHL, SHR, SAL, SAR
SHL and SHR instructions (SHift Left and SHift Right) make the shift operation of a value.
Shift consists in iterating through the specified number of bit positions. For example, if a log contains the binary value 01101101, shift to the left by one position is 11011010; the shift to the left by two positions is 10110100 (the first two bits are "pushed out", while the bottom two bits are filled with 0. Shift right by 1 bit is 00110110; the shift to the right by 2 bit is 00011011 (this time are pushed out the bits, and zeros are added from the left).
SHL and SHR has 2 operands; the first is a register or memory value (8, 16, 32 or 64 bits), and is the destination; the second operand can be register CL, or an immediate 8-bit unsigned (i.e. between 0 and 255), and represents the number of positions you want to shiftare the destination. The second operand are considered only the low order bits 5 (or 6 If the target has 64 bits), so that the counter of the number of positions between 0 and 31 (between 0 and 63 if the target has 64 bit).
SHL and SHR with a different counter from 0 change flags (the details can be seen in the manual); in particular, the CF is equal to the last bit that was pushed out.
Examples:
Code:
shl rax, 1
shr ebx, cl
shl word ptr[r12], 13
shr cl, al ;WRONG! The only valid register second operand is clFrom the arithmetical point of view, a shift to the left by n bits is equivalent to multiplying an unsigned number for 2n; a shift to the right by n bits is equivalent to a Division (with truncation) of an unsigned number for 2n. The use of shift to avoid multiplications and divisions (mainly) is considerably more efficient. Obviously the shift you can use for other purposes bit manipulation
If you want to perform multiplication is division by powers of 2, signed numbers using the instructions SAL (Arithmetical Left Shift) and SAR (Aritmetical Right Shift). The syntax of operands is the same, and also the functions are similar. In fact, SAL is an alias of SHL and does not differ in anything (the opcode is only one, not two different instructions). SAR, instead, behaves as SHR, except that the bits that "come" from left are filled in with the value of the sign bit of the original operand. So while the shift to the right by one bit of 10011010 01001101 shift is arithmetic, is 11001101. Note that binary 10011010 equals decimal -102, while 11001101 is equal to -51 (half!).
The result of the SAR with no counter is equal to that of IDIV with 2n splitter only for positive numbers or when the Division is correct; in fact, while SAR truncates for defect, IDIV truncates toward 0 (so to excess in the case of negative numbers). For example, if you use IDIV to split -9 to 4, the result is -2 and the rest -1 (note that this is not consistent with the mathematical definition of the Division with remainder, where else is always positive). Using SAR for -9 shiftare instead of 2 bits, the result is -3 (and the rest, which in this case is not calculated, is 3).
Code:
sar rax, 2 ;shift arithmetic of 2, equivalent to divide by 4ROL and ROR
The rotations are very similar to shift; the syntax of ROL (ROtate Left) and ROR (ROtate Right) is the same as SHL and SHR. The difference is that the bits "driven out" from a fall on the other side. With the same example as before, left rotation by a bit of 01101101 is 11011010. Right rotation is 10110110. In this case, the CF is set as the last bit pushed out.
Control instructions
CMP and testing
The CMP instruction (CoMPare) has exactly the same syntax of SUB. In fact also carries out the same operation, except for one detail: does not change the target log. The only effect is to update the status flags based on the result of the subtraction between the first and the second operand. Typically it is used to compare two numbers before a conditional jump statement (see below).
Code:
cmp rax, rbx ;compare rax and rbxThe TEST statement, similarly, has the same syntax and the same function AND education; in this case, without modifying the target log, but only changing the flags. You can use, for example, to see if some bits of a value is 1 or 0:
Code:
test al, 8 ;set the ZF if the fourth from last bit is 0A classic use is to verify if a register that is 0 or not:
Code:
test rcx, rcx ;set the ZF if rcx is 0CMP and tests are useful especially with conditional jump instructions.
Data conversion instructions
MOVZX, MOVSX, MOVSXD
MOVZX instructions (MOVe with Zero eXtend), MOVSX (MOVe with Sign eXtend), MOVSD (MOVe with Sign eXtend DWORD search) are used to perform conversions to get smaller in larger data. All require two parameters, the first one (the target) is a register, the second (the source) a register or a memory value.
The first parameter of MOVZX and MOVSX can be 16, 32 or 64 bits, while the second can be 8 or 16 bit (but cannot be both 16 bit). MOVZX zero-extends the source and saves the result in the destination. MOVSX usa a sign-extension. Examples:
Code:
movzx ax, byte ptr [rdi]
movsx eax, byte ptr [rdi]
movzx rax, byte ptr [rdi]
movsx eax, word ptr [rdi]
movzx rax, word ptr [rdi]
movsx rax, dword ptr [rdi] ;WRONG! The second operand may notThe MOVSXD statement exists only in x 64, and serves to extend (with sign) an entire 32 64 bit from to. The first operand is a 64-bit register, the second a register or a memory value to 32 bits. Example:
Code:
movsxd rax, ecx ;extends ecx in raxThere is no instruction designed to make an unsigned extension. The most attentive will have already figured out why: just a simple MOV with 32-bit destination. In fact, x 64, operations on 32 bit registers are zero-extended automatically, it can make sense a statement (at first glance silly) like this:
Code:
mov ecx, ecx ;copy ecx in ecx (zero-extends in rcx!)Flow control statements
The flow-control statements are statements that allow you to change the Instruction Pointer, making a procedure call (CALL/RET), to jump (JMP) or a conditional jump (Jcc).
The flow control statements (except RET) take a parameter that is more frequent in cases of an address relative to RIP. This displacement can be large, up to 32 bit (with sign), so this form of addressing specifies distant destinations allows up to 2 GB from the current statement.
Assemblers, however, you take the load to calculate the correct displacement, allowing you to specify the destination through a symbolic name said label (label).
JMP
The JMP (JuMP) instruction performs an unconditional jump to the destination specified by the operand. In its most common form, the operand is an 8-bit displacement to (near jump) or 32 bits (short jump). Near and short jump allow jump only within the same segment; the far jump (which we don't care about), instead, allow you to jump to a destination of another segment.
In MASM and other assembler, obviously not you write directly to the displacement, but rather indicates the name of a label, leaving the task of coding to the assembler. For example, an infinite loop could have this structure:
Code:
start: ;this is a label
...
;[Code that does something]
...
jmp start ;jump to startno alternative, the operand of a JMP can be a log or a value in memory, that represents the target of the jump (which is the new value of rIP):
Code:
lea rcx, label; in rcx load a pointer
jmp rcx; jumps to the address contained in the rcxOr:
Code:
jmp qword ptr [rax]; jumps to the address contained in [rax]JCC
The family of Jcc instructions (Jump if condition) allows to perform branching, i.e. of jumps that are made if a condition is true, ignored otherwise. The condition is checking the State of one or more status flags. As JMP, Jcc also have only one operand, which can only be a relative displacement (therefore can only be short and near).
See the list of conditional jump instructions; in total there are 16 different instructions, but the mnemonics are more effective, because of the many synonyms:
Were invented many synonyms to help you choose the most appropriate based on the meaning of the code, in order to improve the readability of source code. Of course the disassembler are not always the most consistent between aliases available, given that cannot understand the meaning of the code.
The names of many of these instructions make sense only if you are after a comparison statement (CMP or SUB, of course), while others specify only which control flags (for example JC, JO and JP).
It should be noted that the terms above/below/less and greater are not synonyms: above and below make sense after a comparison of unsigned integers, while greater and less sense after a signed integer comparison.
Let's see some examples:
Code:
cmp rax, rbx; compare rax and rbx
je label; jump if equal
shr cl, 1; shift right by 1 bit
jc odd; jump if the carry flag is 1, if the bit less
; significant of cl(cl was odd)
xor ebx, r12d
jp parity; jumps if after the xor, bl has an even number of 1 bit
add bx, dx
jz; jumps if the sum is 0
;(numbers were opposed)
cmp rcx, rdx
jna major; jumps if rcx is not greater than rdx
If we consider them; unsigned short
jng; jumps if rcx is not greater than rdx
If we consider them; with sign
or al, cl
js sign; skip if bit 7 of al (the sign bit) is equal to 1
this equates to;(did that, prior to or, the bits of
; at least one of the sign two instructions was 1,
; still, that at least one of the two was negative)With conditional jump instructions you can create all the high-level constructs.
A type code
Code:
IF (a == b) THEN
something;
ELSE
something else;Becomes something like (assuming rax and rbx are a and b):
Code:
cmp rax, rbx
jne something else
something:
;...
; IF branch code
;...
jmp after
something else:
;...
; ELSE branch code
;...
after:A loop to repeat code 100 times you write usually as follows:
Code:
mov ecx, 100 ;ecx is counter (needless use rcx). Use
;this register as counter is not required
;but is standard
loop:
;...
;loop code
;...
dec ecx ;decrements the counter
jnz ciclo ;jump if not 0Of course you can translate into assembly language any high-level construct.
CALL and RET
The instructions CALL and RET (RETurn) are used to implement procedure calls.
Also for the CALL statement versions exist near and far; We will analyze just the first case.
The CALL stack puts the rIP (RIP in x 64, x 86 in EIP) of the next statement (it is called return address, return address). Then behaves similarly to the JMP instruction, jumping to the address specified by its single operand. In this case, the operand can be a 32-bit displacement of (i.e., for those who program a label), a record, or a value in memory.
The RET instruction allows you to continue executing the instruction following the CALL. RET pulls the return address off the stack and sets it as the new rIP.
RET may also have a parameter, an immediate 16-bit unsigned, which is added to the rSP after removing the return address stack. In fact, depending on the calling convention, the caller stack puts some or all the parameters required by the function call; the RET is involved then increase rSP to remove them.
Final Notes
Closes this thread here. I hope to be able to not make boring a subject which, by its nature, is inspiring and very creative and it is necessary to understand the workings of malware analysis tools such as Ollydbg.
Source
Intel documentation : http://www.intel.com/content/www/us/en/processors/architectures-software-developer-manuals.html
AMD documentation : https://en.wikipedia.org/wiki/X86-64#AMD64
Overview of x64 Calling Conventions : https://msdn.microsoft.com/en-us/library/ms235286.aspx
And : my school information over the next two years
Thanks everyone !!!
Attachments
Last edited by a moderator:
