Andy Ful
From Hard_Configurator Tools
Thread author
Verified
Honorary Member
Top Poster
Developer
Well-known
- Dec 23, 2014
- 8,970
Let's assume that we have the below results for the test:
2 AVs with 0 undetected malware
4 AVs with 1 undetected malware
4 AVs with 2 undetected malware
3 AVs with 3 undetected malware
1 AV with 4 undetected malware
It can be very close to probabilities for hypothetical AV when:
p(0) = 0.124 (15.5 * 0.124 ~ 2)
p(1) = 0.264 (15.5 * 0.264 ~ 4)
p(2) = 0.275 (15.5 * 0.275 ~ 4)
p(3) = 0.188 (15.5 * 0.188 ~ 3)
p(4) = 0.095 (15.5 * 0.095 ~ 1)
We can see that these probabilities are approximately proportional to the number of AVs for the concrete amount of undetected malware. The proportionality constant is about 15.5 . We can compare this statistics to the AV-Comparatives Malware test for March 2020:
3 AVs with 0 undetected malware (F-Secure, G Data, NortonLifeLock)
4 AVs with 1 undetected malware (ESET, K7, TotalAV, Total Defense)
3 AVs with 2 undetected malware (Avast, AVG, Bitdefender)
3 AVs with 3 undetected malware (Avira, Kaspersky, VIPRE)
1 AV with 4 undetected malware (Panda)

 www.av-comparatives.org
www.av-comparatives.org
The difference is minimal. For example, if Norton and Total Defense would miss one malware more, then the results for 14 AVs would be very close to random trials for one hypothetical AV.
It seems that a similar conclusion was made by AV-Comparatives because it awarded all 14 AVs.
Edit.
It seems that the same conclusion can be derived from cluster analysis made in the report:
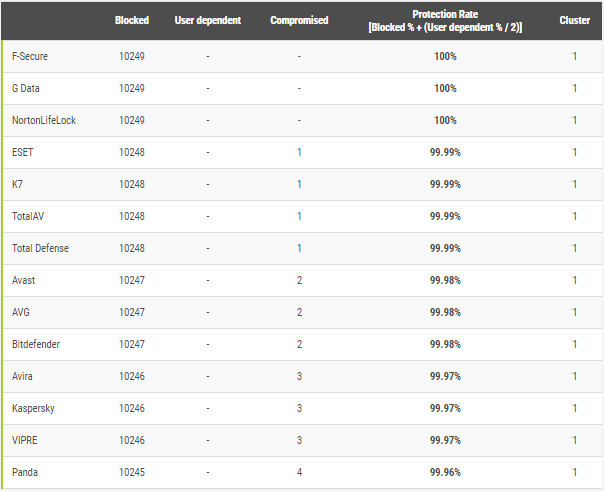
The AVs mentioned in my statistical model belong to the cluster one (see at the last column) and were avarded. Other AVs belong to other clusters.
Here is what AV-Comparatives say about the importance of clusters:
"Our tests use much more test cases (samples) per product and month than any similar test performed by other testing labs. Because of the higher statistical significance this achieves, we consider all the products in each results cluster to be equally effective, assuming that they have a false-positives rate below the industry average."
Real-World Protection Test Methodology - AV-Comparatives (av-comparatives.org)
2 AVs with 0 undetected malware
4 AVs with 1 undetected malware
4 AVs with 2 undetected malware
3 AVs with 3 undetected malware
1 AV with 4 undetected malware
It can be very close to probabilities for hypothetical AV when:
- k = 60 (number of samples that compromised the hypothetical AV on the large pule of samples 300000);
- m = 300000 (the number of samples in the large pule of samples);
- n = 10250 (number of samples included in the AV Lab test);
p(0) = 0.124 (15.5 * 0.124 ~ 2)
p(1) = 0.264 (15.5 * 0.264 ~ 4)
p(2) = 0.275 (15.5 * 0.275 ~ 4)
p(3) = 0.188 (15.5 * 0.188 ~ 3)
p(4) = 0.095 (15.5 * 0.095 ~ 1)
We can see that these probabilities are approximately proportional to the number of AVs for the concrete amount of undetected malware. The proportionality constant is about 15.5 . We can compare this statistics to the AV-Comparatives Malware test for March 2020:
3 AVs with 0 undetected malware (F-Secure, G Data, NortonLifeLock)
4 AVs with 1 undetected malware (ESET, K7, TotalAV, Total Defense)
3 AVs with 2 undetected malware (Avast, AVG, Bitdefender)
3 AVs with 3 undetected malware (Avira, Kaspersky, VIPRE)
1 AV with 4 undetected malware (Panda)

Malware Protection Test March 2020
The Malware Protection Test March 2020 assesses program’s ability to protect a system against malicious files before, during or after execution.
 www.av-comparatives.org
www.av-comparatives.org
The difference is minimal. For example, if Norton and Total Defense would miss one malware more, then the results for 14 AVs would be very close to random trials for one hypothetical AV.
It seems that a similar conclusion was made by AV-Comparatives because it awarded all 14 AVs.
- Bitdefender
- ESET
- G DATA
- Kaspersky
- Total Defense
- VIPRE
- Avast*
- AVG*
- Avira*
- F-Secure*
- K7*
- NortonLifeLock*
- Panda*
- Total AV*
Edit.
It seems that the same conclusion can be derived from cluster analysis made in the report:
The AVs mentioned in my statistical model belong to the cluster one (see at the last column) and were avarded. Other AVs belong to other clusters.
Here is what AV-Comparatives say about the importance of clusters:
"Our tests use much more test cases (samples) per product and month than any similar test performed by other testing labs. Because of the higher statistical significance this achieves, we consider all the products in each results cluster to be equally effective, assuming that they have a false-positives rate below the industry average."
Real-World Protection Test Methodology - AV-Comparatives (av-comparatives.org)
Last edited:

